ОПРЕДЕЛЕНИЕ ЦЕНТРА ТЯЖЕСТИ СЕЧЕНИЯ КОЛОННЫ

Даже во времена современного строительства и проектирования нередко приходится слышать об аварийном состоянии и разрушении некоторых зданий. Очень часто это приводит если не к человеческим жертвам, то к большим финансовым потерям. Именно поэтому выбранная нами тема является очень актуальной.

Цель нашей научной работы состоит в том, чтобы вывести формулу, определяющую зависимость координат центра тяжести расчетного сечения от глубины проникновения трещины в тело балки. Проще говоря, рассчитать координаты нового, смещенного центра тяжести.

Геометрические характеристики несущих элементов принято определять относительно осей, проходящих через центр тяжести сечения. Однако в железобетонных колоннах и балках в процессе работы под действием нагрузок могут возникать трещины. Вследствие этого процесса сечение поврежденной балки уменьшается на площадь трещины. Соответственно смещается и центр тяжести сечения. Его начальное положение находится на пересечении осей симметрии.

Рассмотрим колонну квадратного поперечного сечения, на которую сверху действует продольная сила N и одинаковые поперечные силы Q_y и Q_z. В этом случае трещина будет двигаться параллельно диагонали BD сечения колонны.

Линейное уравнение прямой, параллельной данной диагонали, можно записать в виде:

Y + Z+ K = 0 , (1)

где K — модуль расстояния от начала координат в точке O до линии (1) вдоль одной из осей. При K = h линия (1) касается сечения в точке A. При  K < h — линия пересекает сечение. Пусть K < h. Центр тяжести нового сечения определяется по формуле:

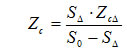. (2)

Вследствие симметрии аналогичная формула будет применяться и для расчета координаты Y_c. В (2):

, (3)

, (4)

. (5)

Подставляя формулы (3),(4),(5) в (2) получим окончательное уравнение:

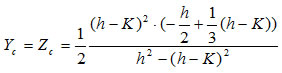. (6)

То есть, центр тяжести смещается от точки O по диагонали AC, в зависимости от K по уравнению (6). Выражение d = (h - K) — характеризует глубину проникновения трещины.

Подведем итог: для квадратных колонн, находящихся под действием равных поперечных нагрузок, получена аналитическая зависимость положения центра тяжести поврежденного сечения в зависимости от площади образовавшейся трещины. 

Автор:  Шеина Елена, 10 класс
Научный руководитель: Игонина И.Н., учитель физики