ПОСТРОЕНИЯ ОДНИМ ЦИРКУЛЕМ

Среди бесчисленных задач на построение встречаются такие, в которых построение требуется произвести одной линейкой или одним циркулем. Однако давно известно, что отсутствие линейки не сужает круга возможных построений: всякое построение, выполнимое циркулем и линейкой, можно проделать одним циркулем.

Идея о построении с помощью одного циркуля была выдвинута еще итальянским ученым. В 1672 году появилась книга «Euclidus Danicus» датского геометра Георга Мора. В ней он показал, что все задачи, которые сводятся к квадратным уравнениям, можно решить геометрически с помощью одного циркуля. Более чем через 100 лет, в 1797 году, эта задача была вновь поставлена и решена итальянцем Лоренцо Маскерони. Соответствующее утверждение называют теперь теоремой Мора — Маскерони.

Разумеется, нельзя провести циркулем прямую, поэтому все рассматриваемые задачи на построение должны состоять в построении некоторой точки (на плоскости).

Теорема. Предположим, что точка М может быть построена по точкам А1...... An при помощи циркуля и линейки. Тогда точка М может быть построена по точкам А1, .... Аn при помощи одного циркуля.

Чтобы доказать эту теорему, посмотрим, какие построения производятся линейкой. С помощью линейки можно провести через две данные точки прямую и найти ее точки пересечения с ранее построенными прямыми и окружностями. Но так как с самого начала нам были даны только точки, всякая ранее построенная прямая была некогда проведена через две еще ранее построенные точки, и всякая ранее построенная окружность имеет своим центром ранее построенную точку. Таким образом, в процессе Построения линейка применяется только к решению одной из двух следующих задач:

Задача 1. По данным точкам А, В, С, D найти точку пересечения прямых АВ и СО.

Задача 2. По данной окружности S с данным центром О и данным точкам А и В найти точки пересечения окружности S с прямой АВ.

Примеры задач, использующие построения одним циркулем .

Задача 3. Даны (различные) точки А и В. Построить на луче АВ точку С такую, что АС=2АВ.

Построение (рис. 1). Проведем через точку А окружность с центром В. На этой окружности трижды отложим отрезок АВ, начиная от точки А.

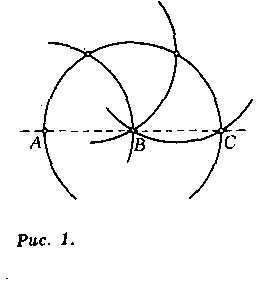
Получившаяся при третьем откладывании точка С удовлетворяет требова­ниям задачи.

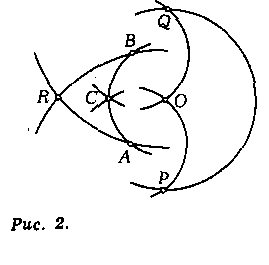
Задача 4. Дана окружность с центром О и дуга АВ на ней. Построить точку, делящую эту дугу пополам.

Построение (рис. 2). Через точ­ку О проведем окружности с центрами А и В. Проведем окружность с центром О радиусом АВ. Возьмем две точки: Р и Qпересечения этой окруж­ности с двумя построенными; тогда дуги ОР и OQравны дуге АВ. Затем через точки В и А проведем окруж­ности с центрами Р и Qдо их пересече­ния в точке R. Наконец, радиусом ОR проведем окружность с центром Р или Q. Точка С пересечения этой окружности с дугой АВ и будет искомой.

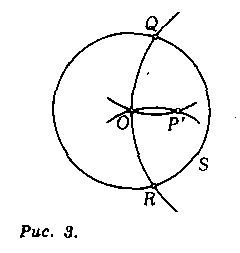
Задача 5. Дана окружность S с центром О и точка Р≠О, точка Р лежит вне окружности. На луче ОР построить точку Р' такую, которая симметрична точке Р относительно окружности.

Точка Р лежит вне окружности S(рис. 3). Проведем через точку О окружность с центром Р. Пусть Qи R — точки ее пересечения с окруж­ностью S. Проведем через точку О окружности с центрами Qи R. Отличная от О точка пересечения этих окружностей и есть искомая точка Р'.

Мне хотелось бы также отметить, что одной линейкой можно проделать не всякое построение, выполнимое циркулем и линейкой. Существует, однако, поразительная теорема Штейнера, со­гласно которой все построения, выпол­нимые циркулем и линейкой, могут быть проделаны одной линейкой, если на листе предварительно нарисована окружность и отмечен ее центр.

Значит, если вы собирались делать построения циркулем и линейкой и за­были дома линейку, не беда — можно обойтись одним циркулем; если же вы забыли циркуль — попросите его у товарища и нарисуйте им одну окружность, предварительно пометив ее центр; после этого вы можете построить что угодно одной линейкой. (Хуже, конечно, если вы забыли дома и циркуль, и линейку — здесь уж наука бессильна вам помочь.)

Автор:  Амиров Эльдар, 11ЛН класс
Научный руководитель: Гуренкова Людмила Кирилловна